플로이드 와샬 알고리즘 [ Floyd Warshall ]
in algorithm / Algorithm on Algorithm, Sort, Github, Git Last modified at:
* 특징
- 다익스트라와 같은 최단 경로를 찾는 알고리즘
- 다익스트라는 하나의 정점에서 출발했을 때, 다른 모든 정점에 대해서 최단 겨올를 구하는 알고리즘인 반면에, 플로이드 와샬은 모든 정점에서 모든 정점으로의 최단 경로를 구합니다.
- 거쳐가는 정점을 기준으로 알고리즘을 수행합니다.
점화식
- i행과 j열의 (i,j) 원소는 정점 i로부터 정점 j까지의 최단 경로를 나타냅니다.
- 동적 계획법 (Dynamic Programming)으로 진행되어진다.
- 점화식은 dist[i, j] = min(dist[i,j], dist[i, n] + dist[n, j]) 입니다.
- + 정점 i에서 j로 가는 경로와 / i에서 n , n에서 j로 가는 경로 중 더 빠른 경로로 업데이트 합니다.
* 예시
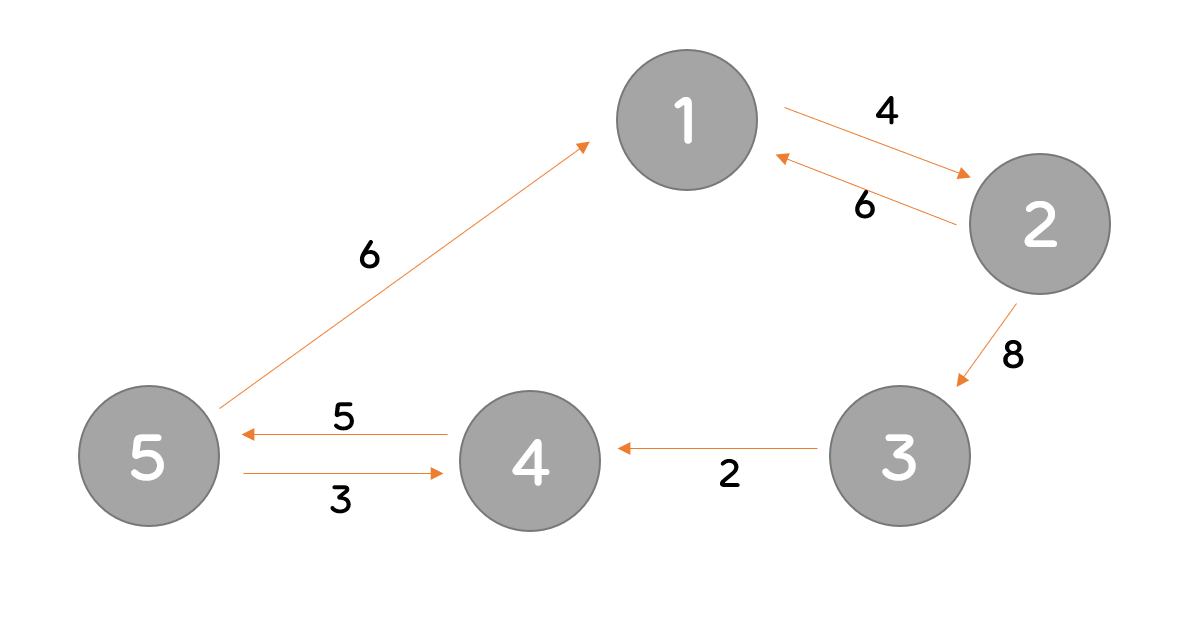
- 위의 그래프로 플로이드 와샬이 어떻게 진행되는지 보겠습니다.
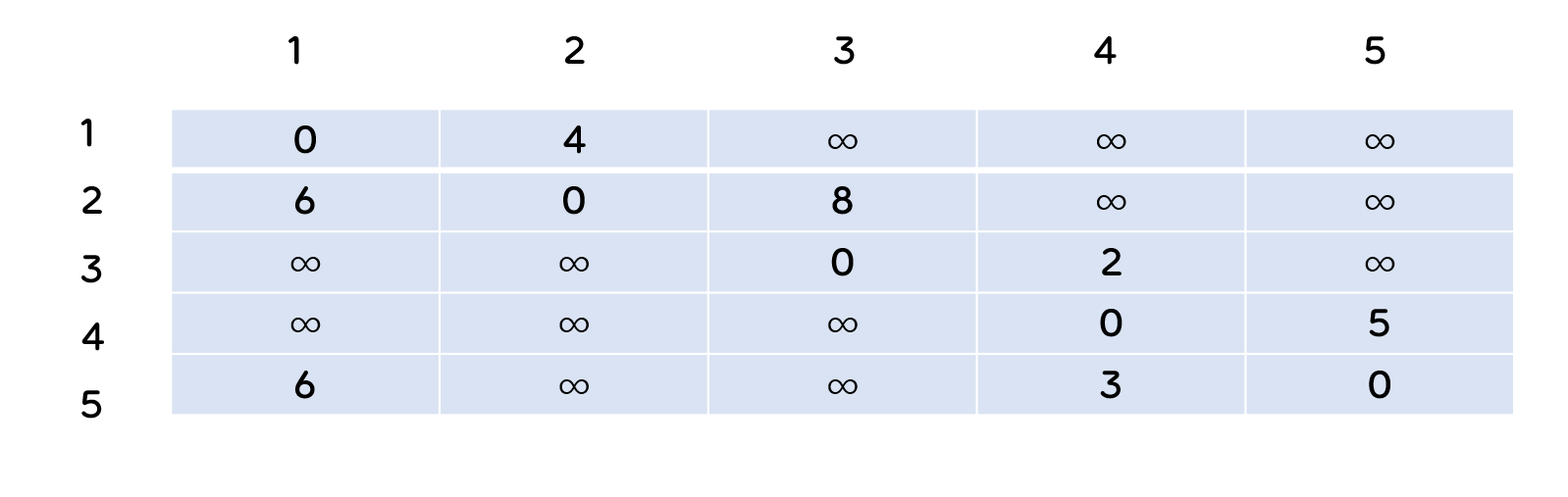
- 다음과 같이 현재 초기의 노드들에 대한 초기 비용이 계산된 이차원 배열이 나타나게 됩니다. ∞는 현재 기준에서 갈 수 없는 것을 의미하고 자기 자신은 0으로 나타나게 됩니다.
<1의 노드를 지나갈 때 입니다.>
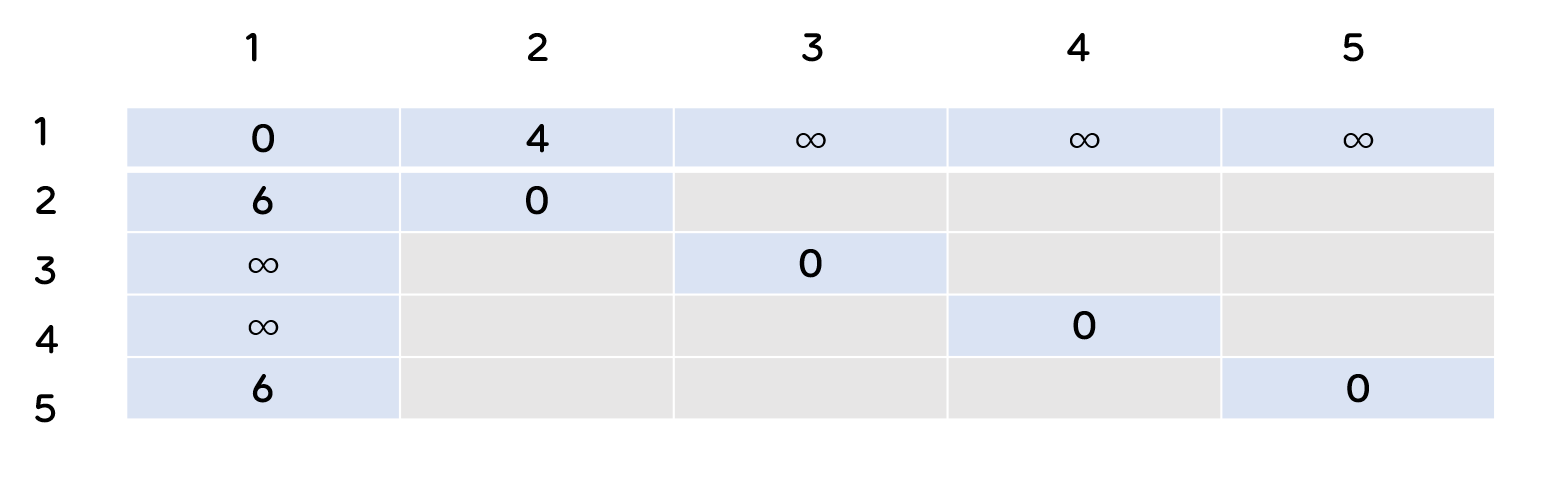
- 위와 같이 비어있는 부분을 업데이트 하게 됩니다.
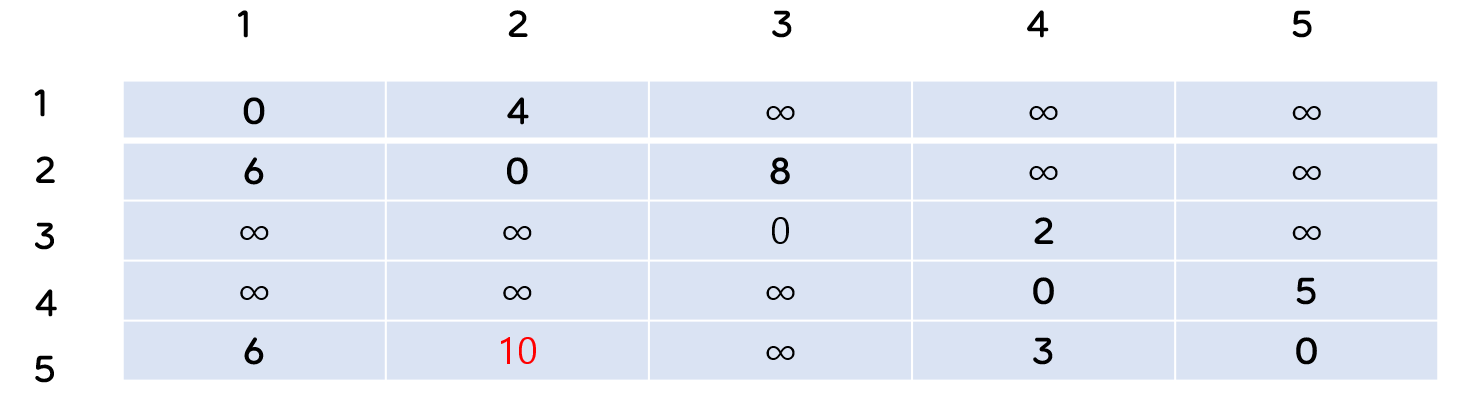
- 다음과 같이 1의 노드를 경유하여 갈 수 있는 곳인 5 -> 1 -> 2가 업데이트 되게 됩니다.
<2의 노드를 지나갈 때 입니다.>
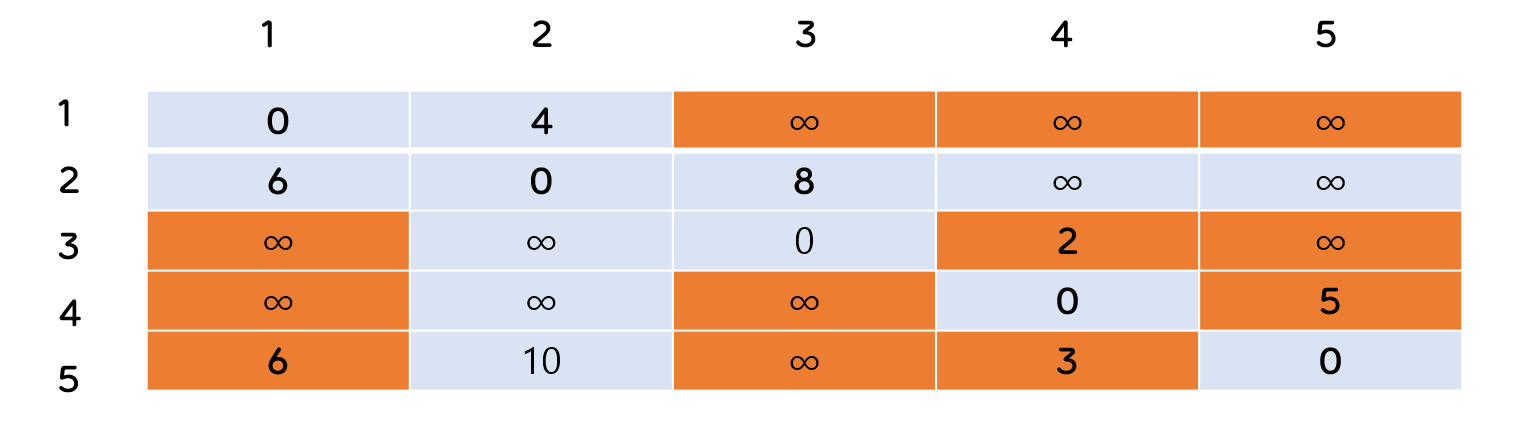
- 다음과 같이 2의 노드구간과 자기 자신을 제외한 곳이 업데이트 기준이 되는 곳 입니다.
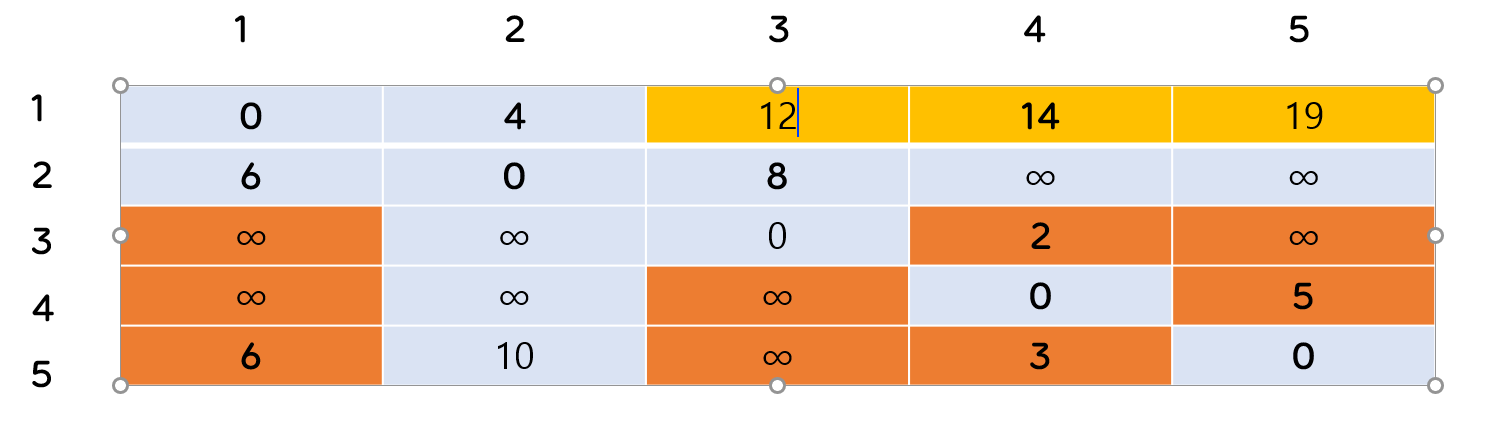
- 다음과 같이 노드 2를 거쳐가는 1 -> 2 -> 3, // 1 -> 2 -> 3-> 4, // 1-> 2-> 3-> 4-> 5 구간이 업데이트 되었습니다.
최종
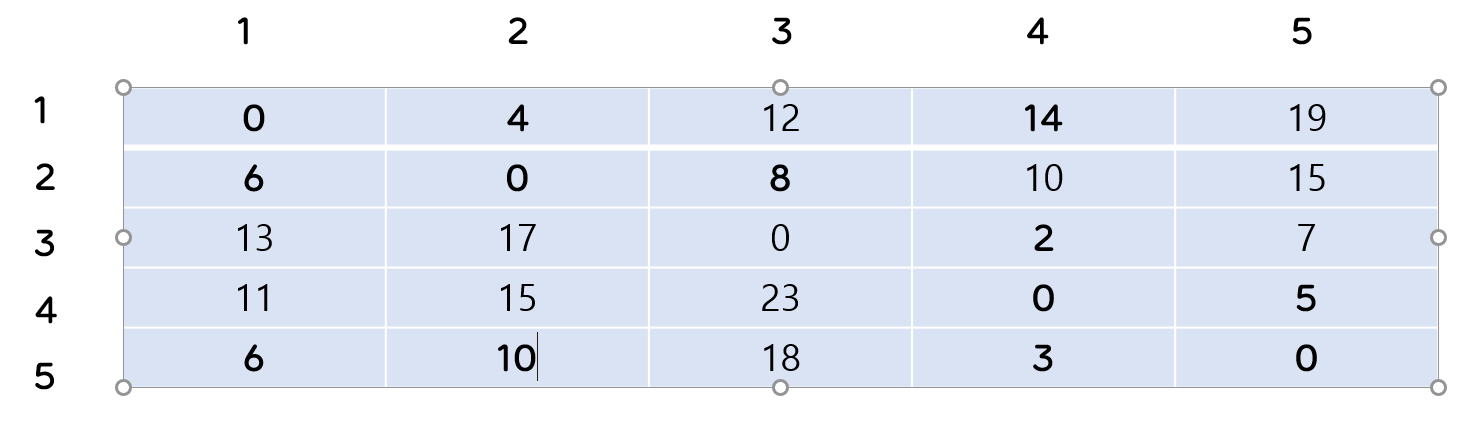
- 계속해서 반복하시게 되면 위와 같이 나타나게 됩니다.
* 예시 코드
* 참고 사이트
나동빈님의 Floyd Warshall 포스팅을 참고하였습니다.