:no_entry_sign: 시간 복잡도 [Time Complexity]

in cs on Cs, Data structure, Tech-interview

CS 첫번째 게시물로 시간복잡도에 대해서 공부하고 남기는 게시글입니다.

시간복잡도는 특정 알고리즘이 문제를 해결하는데 걸리는 시간을 의미합니다. 같은 문제라도 O(n^2)이 걸리는 알고리즘과 O(n)이 걸리는 알고리즘이 있을 수 있습니다. 둘 중 더 빠른 알고리즘을 사용하는 것이 좋습니다. 이와 같이 특정 문제에서 어떤 알고리즘을 사용해야하는지 파악하는 데 중요하다고 생각합니다.

:question: 다음과 같은 내용을 공부합니다.

  • 시간복잡도 (Big-O, Big-Omega, Big-Theta)

  • 공간복잡도

:dash: 시간복잡도의 종류와 Big-O

  • Big-O(빅-오) : 최악의 경우를 나타냅니다.

  • Big-Omega(빅 오메가) : 최선의 경우를 나타냅니다.

  • Big-θ(빅-세타) : 최선과 최악의 중간인 평균을 나타냅니다.

:raising_hand: 다른것을 사용하지 않고 Big-O를 사용하는 이유는?

시간 복잡도의 가장 큰 개념은 적어도 이 시간안에 끝날 것을 의미합니다. 따라서, 최선과 평균을 나타내 최소 ~ , 평균 ~ 이 시간안에 해결된다는 것보다 “최악의 경우 이 시간안에 끝난다”를 고려해서 대응하는 것이 좋기때문에 Big-O 표기법을 사용합니다.


:eyes: 예시를 들어서 설명해보겠습니다.

어떤 알고리즘을 실행하는데 최선의 경우는 1초, 평균은 10초, 최악은 100초라고 가정하겠습니다.


:exclamation: 최선의 경우를 고려한 경우

  • 해당 알고리즘이 10번 실행됐습니다.
  • 우리가 원하는 실행시간은 10초이지만 실제 실행된 시간은 10초가 넘어버리게 된다면, 어디에서 문제가 발생했는지 정확하게 모르게 됩니다.


:exclamation: 평균의 경우를 고려한 경우

  • 최선의 경우를 고려한 경우와 상황이 같습니다.


:exclamation: 최악의 경우를 고려한 경우

  • 해당 알고리즘이 10번 실행되어서 1000초가 걸려서 문제가 생겼습니다.
  • 최악의 경우를 대비해서 시간 복잡도 계산을 하였으므로, 해당 알고리즘의 문제를 찾을 수 있게 됩니다.
  • 따라서 우리는, 최악의 경우가 발생했음을 가정하고 계산하는 것이 바람직합니다.

:speech_balloon: Big-O 표기법의 종류

  • O(1)
  • O(N)
  • O(logN)
  • O(n^2)
  • O(2^n)

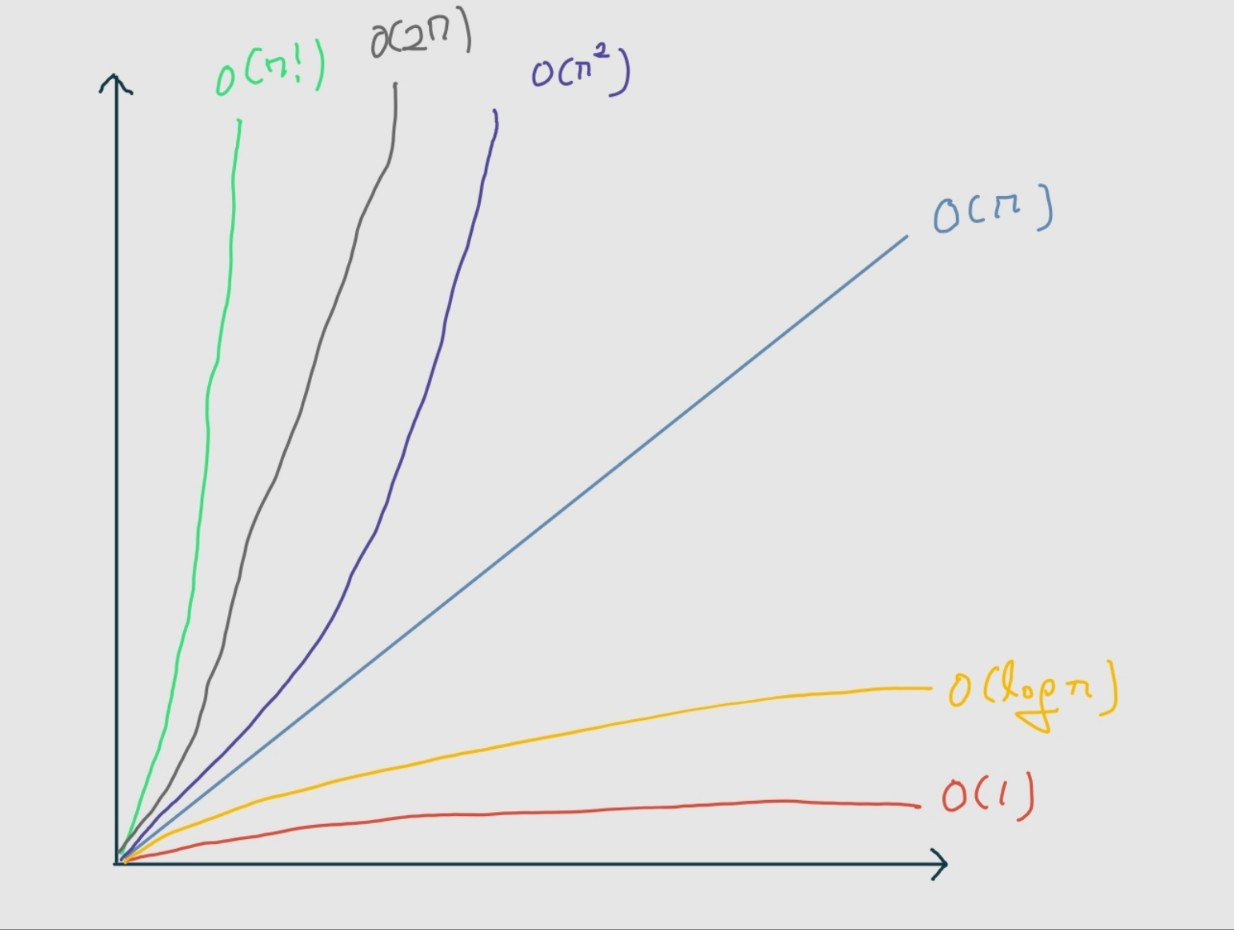
image

:exclamation: 시간복잡도에 대한 작성법 및 설명

빅오 표기법의 작성법은 가장 큰 차수의 n 이외의 것들을 제외하게 됩니다. 예를 들어 O(n^2 + 1000n + 100)이라는 알고리즘이 있다고 가정합니다. n의 입력 개수가 많아져서 10억이라고 가정을 한다면, 1000n + 100은 그렇게 큰 비중을 차지하게 되지 않기 때문입니다. 따라서 해당 알고리즘은 O(n^2)이라고 표시합니다.

:sparkles: O(1)

  • O(1)는 상수시간으로, 입력값의 크기와 관계 없이 즉시 값을 출력할 수 있음을 의미한다.

:sparkles: O(N)

  • 입력 데이터의 크기에 비례해서 처리 시간이 증가합니다. 대표적으로 다음과 같은 for문이 있습니다.

:sparkles: O(logN)

  • 데이터 크기가 커질수록, 로그 시간만큼 짧아집니다. 대표적으로 이진탐색이 있습니다.

:sparkles: O(n^2)

  • 입력값의 n의 제곱수의 비율로 증가하는 것을 의미합니다.
  • 예를 들어, 2차 for문이 있습니다.

:sparkles: O(2^n)

  • 정확히는 c^n이라고 말하며, 기하급수적으로 시간이 증가하는 것을 의미합니다.

:raising_hand: O(1)은 O(N^2) 보다 무조건적으로 빠른가요?

먼저 정답을 말씀들리면 아닙니다.

빅오표기법은 기본적으로 상수를 무시합니다. 알고리즘의 데이터가 커져서 O(1)이 1000번 일어나도 O(1)으로 표시합니다. 예를 들어, Big-O 표기법에서 실제 O(N/2)도 O(N)으로 표시한다. 이러면 100번을 진행했을 경우 O(1)의 기준, 100번이 진행되고, O(N)의 기준 50번이 진행되므로 O(N)이 빠른 경우도 있다. 하지만 데이터가 많아질수록, O(1)보다 덜 효율적인 지점이 생기게된다.

:no_entry_sign: 공간 복잡도 [Space Complexity]

공간 복잡도란, 프로그램을 실행시킨 후 완료되는데 필요한 자원의 양을 의미합니다. 총 공간은 고정 공간과 가변 공간 요구로 나타낼 수 있습니다. 여기서 고정 공간은 입력과 출력의 횟수나 크기와 관계없는 경우(변수, 고정 크기의 배열 등)을 의미합니다. 가변 공간은 해당 알고리즘에 필요한 공간, 예를 들어 함수가 재귀호출을 할 경우 추가되는 동적 공간을 의미합니다.

:ok_woman: 공간 복잡도 예시

  1. 일반적인 형태
  • 다음과 같은 경우, 반복문이 n번 반복하더라도 지역변수이고, 다른 변수에 영향을 주지 않기때문에 공간복잡도는 O(1)입니다.
  1. 재귀함수
  • 반면에 재귀함수의 경우, n이 1이 될때까지 함수를 호출하게 됩니다. 그렇기 때문에 스택에는 n의 함수 ~ 1의 함수가 쌓이게 되므로 다음의 경우 O(n)의 공간복잡도를 가지게 됩니다.