[코딩테스트 스터디 - 알고리즘 #1 Union - Find Algorithm]
in study on Ct, Union-find, Github, Git
서로소 집합 [ Disjoint Sets Algorithm ]
- 서로소 집합은 공통집합이 없는 알고리즘입니다.
- 서로소 집합 알고리즘은 union-find 연산으로 이루어지며, 모든 노드는 자신이 속한 집합을 찾을 때 루트노드를 재귀적으로 찾게됩니다.
서로소 집합
서로소 집합 자료구조란 서로소 부분 집합들로 나누어진 원소들의 데이터를 처리하기 위한 자료구조 입니다.
union(합집합) 연산은 2개의 원소가 포함된 집합을 하나의 집합으로 합치고 find(찾기) 연산은 특정한 원소가 어떤 집합에 속해있는지 찾게됩니다.
따라서 union-find 연산을 이용하여 서로소 집합을 표현합니다.
Union-Find
Union-Find란 Djsjoint Sets를 표현할 때 사용하는 알고리즘입니다.
집합을 구현할 때 vector, array, linked list, tree를 활용할 수 있다.
Union-Find 연산
-
make-set(x)
- 초기화, x를 유일하게 가지는 집합을 만든다.
- union(x, y)
- x가 속한 집합과 y가 속한 집합을 합치는 과정
- find(x)
- x가 속한 집합의 루트노드를 반환해서, 어떤 집합에 속해있는지 알아낸다.
Union-Find 알고리즘 배열 VS 트리
- 배열
- Array[i] = i // i번 원소가 속하는 집합의 번혼
- make-set(x) // Array[i]와 같은 개념
- union(x, y) // 배열 크기를 돌면서, y의 집합 번호(루트 노드)를 x의 집합 번호로 변경하고, 결과적으로 O(N)의 시간 복잡도 발생
- find(x) // x가 속한 집합 번호를 O(1)의 시간으로 찾게된다.
- 트리
- 트리 구조는 같은 집합은 같은 트리내에서 형성되어 있다고 말할 수 있다.
- make-set(x) // 초기 각 노드는 모두 루트 노드로서, N개의 루트 노드 및 자기 자신으로 초기화한다
- union(x, y) // x, y의 루트노드를 찾게되고, 다를 경우 y를 x의 자손으로 넣어 트리를 만든다. 시간복잡도는 O(N)보다 작다.
- find(x) // 루트 노드를 확인하여 같은 집합인지 확인한다. 시간 복잡도는 트리의 높이와 일치한다 O(N-1)
Union-Find 알고리즘 과정
Union-Find의 기본적인 구현
- Union-Find가 어떻게 돌아가는지 간략히 그림으로 나타냅니다.
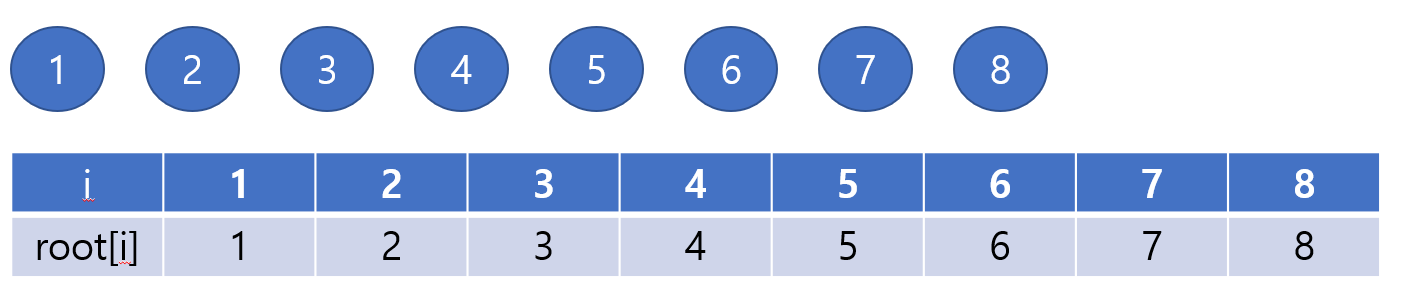
- 위와 같이 처음에 자기 자신을 가리키도록 구성이 되어있습니다.
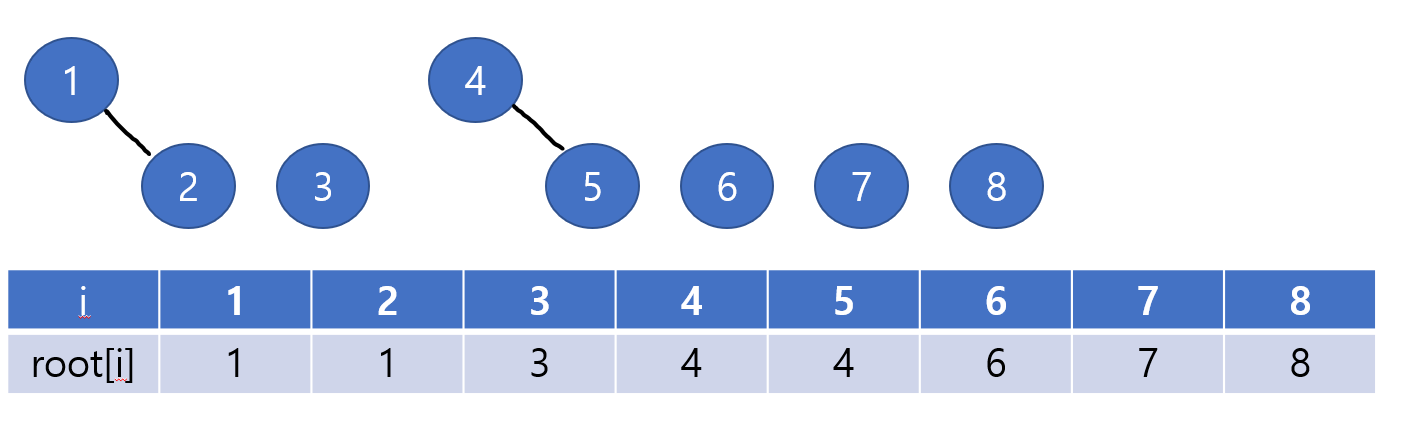
다음과 같이 union(1,2) union(4,5)를 통해서 2의 루트 노드는 1로, 5의 루트 노드는 4로 변경되게 됩니다.
이를 반복하여 자신의 루트노드를 저장하게 되고, find(x) 연산을 통해서 x를 찾아주게 됩니다.
- union(1,2)의 결과로 2는 1의 루트 노드를 저장하게 되고, find(2)로 찾은 결과값은 1이 나오게 됩니다.
Union-Find 관련 문제
백준 - 1817 [ 집합의 표현 ] https://www.acmicpc.net/problem/1717
Refrences
https://zz132456zz.tistory.com/11
https://gmlwjd9405.github.io/2018/08/31/algorithm-union-find.html
https://brenden.tistory.com/33